Sizing gemma3 for TPUv5-n

Acknowledgement : Google Cloud credits are provided for this project :: #AISprint

Practical limits for `gemma3` rollouts and training

on 16Gb HBM TPUv5-1/8

The following set of experiments was carried out with an eye on the Kaggle tunix competition that is being run to get participants to train a gemma2-2B or gemma3-1B model to be a General Reasoner (TM), all within the budget of having a TPUv5-8 instance for a single run of 9 hours.

Some of the key constraints that this imposes are:

Limited to 16Gb HBM on each of the 8 TPUs
Careful choice of batch_size required for maximising rollout throughput
Consideration of how to train models with large vocabularies (like gemma2 and gemma3)

These experiments were mainly done on Kaggle-equivalent GCP machines, set up according the recipe in my previous blog post, since that enabled more certainty in timing of getting a TPU instance (since the Kaggle instances are under high demand, and access is via a queue).

Note that the full code for these experiments is in my 'Aha' GitHub repo, with the python file 1-mem-and-perf.py being in GitHub, but the output of the .ipynb being stored locally (not in the repo, naturally, through the use of jupytext).

Question 1 : What should I import?

import os, time

# Needed to fix some jupyter async issues and memory clean-up
import asyncio, gc  

import numpy as np  # On CPU : used for tokeniser stuff

import jax
import jax.numpy as jnp

from flax import nnx

from tunix.generate import tokenizer_adapter as tokenizer_lib
#from tunix.models.gemma import model as gemma_lib    # gemma2!
#from tunix.models.gemma import params as params_lib  # gemma2!
from tunix.models.gemma3 import model as gemma_lib
from tunix.models.gemma3 import params as params_lib
from tunix.generate import sampler as sampler_lib

import optax
from orbax import checkpoint as ocp
import qwix  # For LoRA

Question 2 : Can I load a `gemma` model?

The Kaggle examples, and even those in the tunix repository are all over the place : loading from Kaggle/tensorflow, HuggingFace (different credentials), etc.

The following code loads a Kaggle model into nnx with the minimum of fuss.

Load the Kaggle credentials (assuming we have a suitable dotenv file - actual Kaggle user won't need this step, as the instances already have their environment variables set correctly):

from dotenv import load_dotenv
if not load_dotenv(override=True):
  load_dotenv('./tpu_dotenv/dotenv', override=True)
print( os.environ['KAGGLE_USERNAME'], os.environ['KAGGLE_KEY'][-4:], )

Download the model (this silently makes use of the environment variables set above, no user interaction is required):

import kagglehub

KAGGLE_MODEL_HANDLE = "google/gemma-3/flax/gemma3-1b-it"  
model_config = gemma_lib.ModelConfig.gemma3_1b()

# Download the model to disk
kaggle_ckpt_path = kagglehub.model_download(KAGGLE_MODEL_HANDLE)

# Create the mesh layout
MESH_COUNTS = (1, 1)  # Default
if NUM_TPUS == 8:
  # in https://www.kaggle.com/code/danielwycoff/dsa-cast-tunix-nolora-from-scratch
  MESH_COUNTS = (1, 4)  # Spread across first 4 TPUs 
  #MESH_COUNTS = (1, 8) # Spread across all TPUs ?
  #MESH_COUNTS = (8, 1) # in https://www.kaggle.com/code/marculera/supervised-fine-tuning-full
mesh = jax.make_mesh(MESH_COUNTS, ("fsdp", "tp"), 
                     axis_types=(jax.sharding.AxisType.Auto,)*2)

# Actually load the model onto the TPU(s)
model_nnx = params_lib.create_model_from_checkpoint(
  os.path.join(kaggle_ckpt_path, "gemma3-1b-it"),
  model_config,  
  mesh=mesh,
)

# Required for Jupyter since orbax uses async in a way that might conflict with Jupyter
await asyncio.sleep(0)  # Sync before going to next cell

Question 3 : Can I make a LoRA version?

And not have two copies in HBM...

The following (from a tunix example) works :

def get_lora_model_qwix(base_model, mesh, rank=RANK, alpha=ALPHA):
  lora_provider = qwix.LoraProvider(
    module_path=(
      ".*q_einsum|.*kv_einsum|.*gate_proj|.*down_proj|.*up_proj|"
      ".*attn_vec_einsum"
    ),
    rank=rank, alpha=alpha,
  )

  model_input = base_model.get_model_input()
  lora_model = qwix.apply_lora_to_model(
    base_model, lora_provider, **model_input, rngs=nnx_rng,
  )

  with mesh:
    state = nnx.state(lora_model)
    pspecs = nnx.get_partition_spec(state)
    sharded_state = jax.lax.with_sharding_constraint(state, pspecs)
    nnx.update(lora_model, sharded_state)

  return lora_model


model_lora = get_lora_model_qwix(model_nnx, mesh=mesh)

del model_nnx  # This will reclaim the HBM (the LoRA version still works)

The following shows the 'speed penalty' for using a LoRA version of the model for rollouts vs just using the base model itself. Note that the LoRA version has little overhead (particularly compared to the difference of choosing batch_size==64 as opposed to batch_size==68, or batch_size==128 as opposed to batch_size==132)

These were done with a consistent steps_max=1024 - which is realistic for the Kaggle tunix competition setting.

Question 4 : What `batch_size` can I use for rollouts?

And how fast are they?

The following is an estimate of the KV cache size, which is allocated during generation but will not be in use when the generation has completed:

def kv_cache_estimate(batch_size, steps_max=(MAX_PROMPT_LENGTH + MAX_GENERATION_STEPS + 32)):
  # https://notes.kvfrans.com/7-misc/rl-infra.html
  return (
    batch_size * steps_max *  # But actual allocation is not dependent on steps_max
    model_config.num_layers * model_config.num_kv_heads * model_config.head_dim
    * 2 # K+V
    * 2 # sizeof(bfloat16
  )

This is the sampler for the generation, which defines how the caching works:

def build_sampler(rollout_model, tokenizer, model_config):  # CACHE_SIZE based on MAX_GENERATION_STEPS
  """NB: Need to pass in the actual model to be used"""
  return sampler_lib.Sampler(
    transformer=rollout_model,
    tokenizer=tokenizer,
    cache_config=sampler_lib.CacheConfig(
      #cache_size  = MAX_PROMPT_LENGTH + MAX_GENERATION_STEPS + 256,
      cache_size  = MAX_PROMPT_LENGTH + MAX_GENERATION_STEPS + 32,
      num_layers  = model_config.num_layers,
      num_kv_heads= model_config.num_kv_heads,
      head_dim    = model_config.head_dim,
    ),
  )

And here is the answer generation (note that there's some left-over garbage collection code):

def generate_answers(question_arr, sampler, steps_max=MAX_GENERATION_STEPS, 
                     temperature=0.7, top_k=50, top_p=0.95, seed=None):
  batch = [
    TEMPLATE.format(system_prompt=SYSTEM_PROMPT, question=q)
    for q in question_arr
  ]
  out = sampler(
    input_strings=batch,
    temperature=temperature, top_k=top_k, top_p=top_p,
    max_generation_steps=steps_max,
    eos_tokens=EOS_TOKENS,
    seed=seed, echo=False,
  )
  text_arr = out.text[:]  # Copy
  del out # Release structure
  gc.collect() #?
  return text_arr

Finally, some results for different batch_size being used:

Total elapsed time:

Per token speed (note the non-linear changes as we go across batch_size==64 and batch_size==128):

HBM usage:

Question 5 : How efficient are parallel feed-forward passes?

When training a full rollout, we can do a parallel feed-foward pass. But these graphs show that this can only handle small batch_size:

Total elapsed time:

HBM usage:

Here, we see that using the standard the gemma feed-forward design quickly fills HBM. This is due to the large size of the logits (because of the size of the vocabulary being used). Can we do this in a smarter way?

Question 6 : Can we feed-forward in parallel sparsely?

This is a rather particular use-case I have in mind... But the technique investigated here is fairly general.

Gemma models have very large vocabulary sizes. So, while their final hidden states are of reasonable size, their logit outputs are HUGE. This makes just 'materialising' the logits very expensive across a parallel feed-forward pass in terms of HBM usage, which in turn quickly reduces the possible batch_size during training.

Here's some sample code for the kind of operations needed to process logits in a non-materialised way (followed by graphs proving that this works):

from functools import partial

@jax.jit
def forward_to_prelogits_no_cache(self_model, tokens, positions, attention_mask):
  new_cache = None
  # Taken from tunix gemma3 code 
  #  https://github.com/google/tunix/blob/main/tunix/models/gemma3/model.py#L918-L938
  x = self_model.embedder.encode(tokens)
  for i, layer in enumerate(self_model.layers):
    layer_name = f'layer_{i}'
    #layer_cache = cache[layer_name] if cache else None
    with jax.named_scope(layer_name):
      layer_cache_discarded, x = layer(
          x,
          positions,
          None, #layer_cache,
          attention_mask,
      )
    #if cache is not None:
    #  new_cache[layer_name] = layer_cache  # pytype: disable=container-type-mismatch

  return self_model.final_norm(x)  # 'x' is the pre-logits stage...
  #if output_hidden_states:
  #  self_model.sow(nnx.Intermediate, 'all_hidden_states', x)
  #logits = self_model.embedder.decode(x)

@partial(jax.jit, static_argnames=['k'])
def compute_chunked_top_k(hidden_states, embedding_matrix, k=128):
  """
  Computes Top-K logits without ever materializing the full [Batch, Seq, Vocab] tensor.
      
  Returns:
      top_vals: [Batch, Seq, K]
      top_inds: [Batch, Seq, K]
  """
    
  # 1. We scan over the Sequence dimension (axis 1).
  # hidden_states needs to be transposed to [Seq, Batch, Hidden_Dim] for easier scanning
  hidden_states_T = jnp.swapaxes(hidden_states, 0, 1)

  def scan_step(carry, x_t):
    # x_t shape: [Batch, Hidden_Dim] (This is the hidden state for 1 timestep)
    
    # Compute logits ONLY for this timestep
    # [Batch, Hidden] @ [Hidden, Vocab] -> [Batch, Vocab]
    # This is 1024x smaller than the full sequence matrix
    logits_t = jnp.matmul(x_t, embedding_matrix.T) 
    
    # Extract Top-K immediately
    vals_t, inds_t = jax.lax.top_k(logits_t, k)
    
    # We don't need to carry anything, so return None
    return None, (vals_t, inds_t)

  # 2. Run the scan loop
  _, (top_vals_T, top_inds_T) = jax.lax.scan(scan_step, None, hidden_states_T)
  
  # 3. Swap axes back to [Batch, Seq, K]
  top_vals = jnp.swapaxes(top_vals_T, 0, 1)
  top_inds = jnp.swapaxes(top_inds_T, 0, 1)
  
  return top_vals, top_inds

# ... 

# make use of top_k logits only (actual logits are not materialised):
prelogits = forward_to_prelogits_no_cache(gemma_model, token_input, positions, attn_mask)
top_vals, top_inds = compute_chunked_top_k(prelogits, gemma_model.embedder.input_embedding, k=128)
#top_vals.block_until_ready()  # for benchmarking

Per token speed for non-materialised logits (note that there isn't so much of a marked lumpy path in batch_size as before):

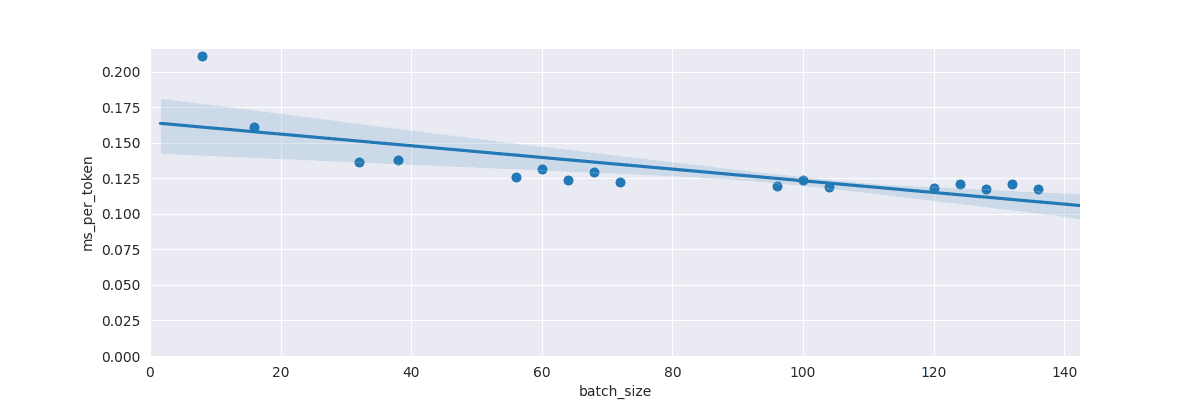
LoRA 1024-step parallel non-materialised per-token speed

HBM usage for non-materialised logits (note that the memory usage is fairly even across batch_size, since the non-materialised logitcs are 'boiled down' to the top_k==128 values, and their indicies. Also, in this graphs the y-axis is offset, it's the slope that's important) :

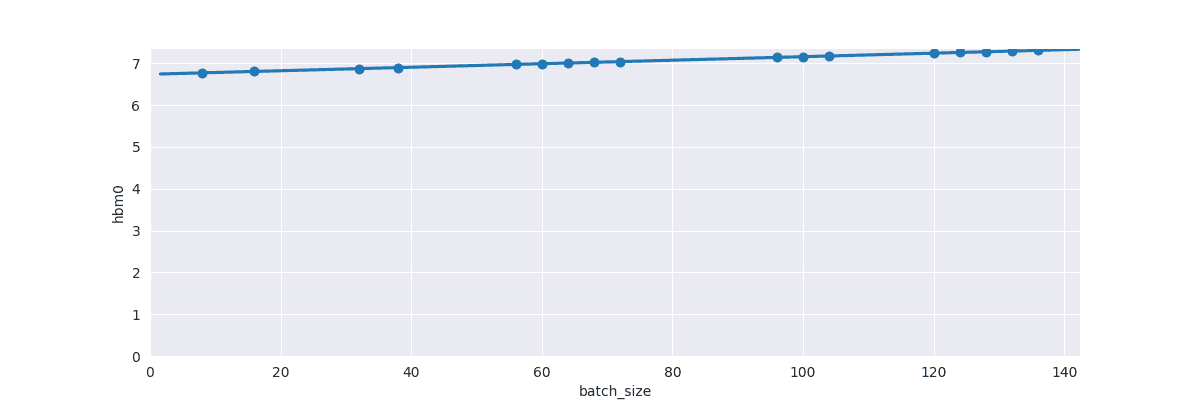
LoRA 1024-step parallel non-materialised HBM usage

Conclusions

There's clearly more to talk about w.r.t the RL training process that we can do efficiently on these TPU instances.

But perhaps my next post on this will be after the Kaggle competition ends...

Practical limits for gemma3 rollouts and training